როგორ გამოვთვალოთ მოსახვევის შემწეობა თქვენი პრესის მუხრუჭისთვის

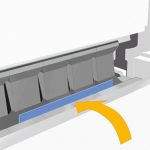
1. დახრის პროცესის გაგება: მარტივი ფაქტები

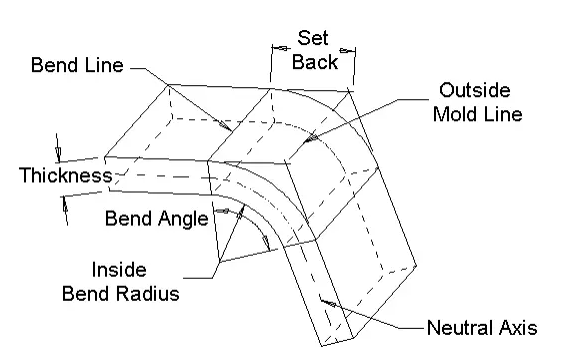
მოსახვევის დაშვება = კუთხე * (T/ 180)* (რადიუსი + K-ფაქტორი *სისქე) მოსახვევის კომპენსაცია = მოსახვევის შემწეობა-(2 * უკან დაყენება)

უკან დაყენება შიგნით = რუჯი (კუთხე / 2) *რადიუსი გარედან უკან = რუჯი (კუთხე / 2)*(რადიუსი + სისქე)

1) მოხრილ ნაწილზე მიღებული რადიუსი გავლენას ახდენს სიგრძეზე, რომელზედაც უნდა მოვჭრათ ეს ნაწილი (მოხრამდე).

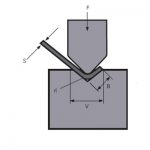
2) მოხრაზე მიღებული რადიუსი 99%-ით არის დამოკიდებული V ღიობზე, რომლითაც ვირჩევთ მუშაობას.

ნაწილის დაპროექტებამდე და აუცილებლად სანამ დავიწყებთ ბლანკების ჭრას, ზუსტად უნდა ვიცოდეთ, თუ რა V ღილაკს გამოვიყენებთ ნაწილს პრეს brake-ზე მოსახვევად.

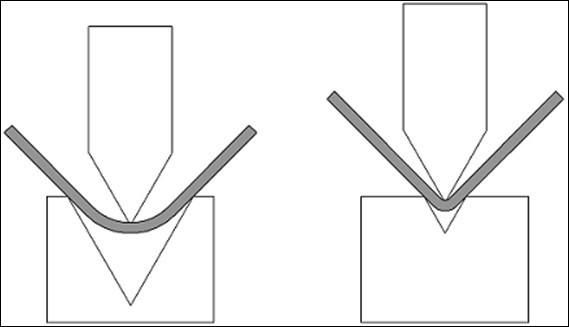
2. როგორ მოქმედებს რადიუსი ბლანკებზე

უფრო დიდი რადიუსი ჩვენი ნაწილის ფეხებს გარესკენ „უძვრება“ და იქმნება შთაბეჭდილება, რომ ბლანკი „ზედმეტად დიდხანს“ იყო მოჭრილი.

უფრო მცირე რადიუსს დასჭირდება ბლანკი, რომელიც უნდა მოიჭრას „ცოტა ხანს“, ვიდრე რადიუსი უფრო დიდი იყო.

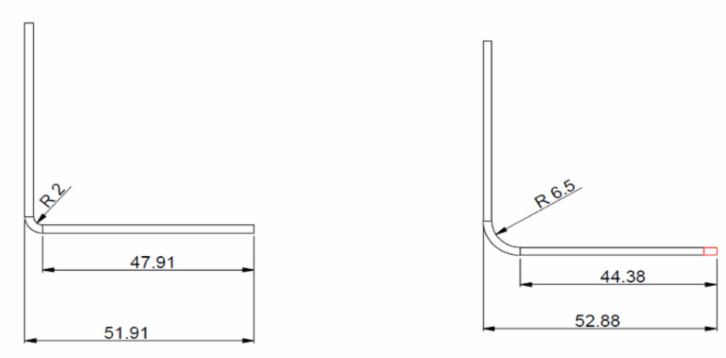
3. Bending Allowance

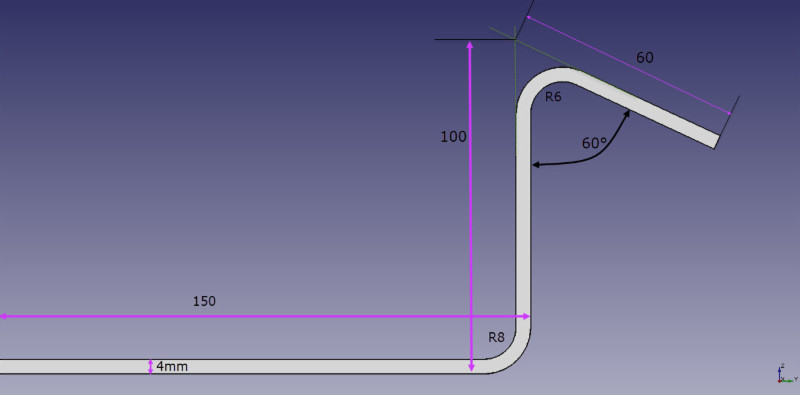
ზემოთ მოყვანილი ფიგურის გაშლილი ბლანკები გამოითვლება შემდეგნაირად:

B = 150 + 100 + 60 + BA1 + BA2

როგორ გამოვთვალოთ BA1 და BA2:

მოსახვევის შემწეობის გაანგარიშება

ნაწილი, რომელიც უნდა შევამციროთ ორივე ფეხიდან, ერთხელ გადაფარვით, ბრტყელი გახდომით, არის ის, რასაც ჩვენ საყოველთაოდ ვიცნობთ, როგორც „მოხრის შემწეობა“ (ან BA განტოლებაში).

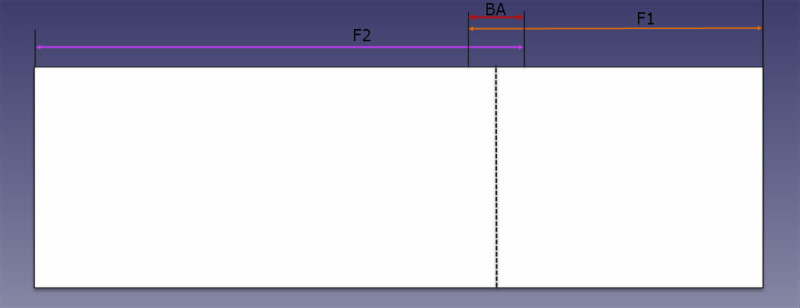
მოსახვევის შემწეობის ფორმულა

BA ფორმულა 90°-მდე მოსახვევებისთვის

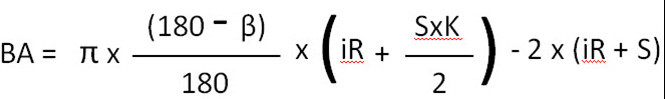
BA ფორმულა მოსახვევებისთვის 91°-დან 165°-მდე

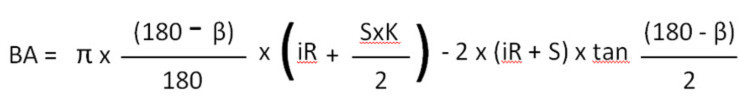
iR = შიდა რადიუსი
S=სისქე
Β = კუთხე
Π = 3,14159265….
K = K ფაქტორი

K ფაქტორი

პრესის მუხრუჭზე მოხრისას ლითონის ფურცლის შიდა ნაწილი შეკუმშულია, ხოლო გარე ნაწილი გაშლილია.

ეს ნიშნავს, რომ არის ფურცლის ნაწილი, სადაც ბოჭკოები არც არის შეკუმშული და არც გაშლილი. ჩვენ ამ ნაწილს "ნეიტრალურ ღერძს" ვუწოდებთ.

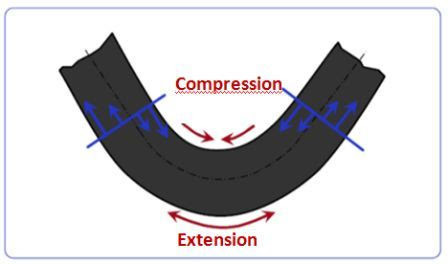
მანძილი მოსახვევის შიგნიდან ნეიტრალურ ღერძამდე არის ის, რასაც ჩვენ ვუწოდებთ K ფაქტორს.
ეს ღირებულება მოყვება ჩვენ მიერ შეძენილ მასალას და მისი შეცვლა შეუძლებელია.
ეს მნიშვნელობა გამოიხატება წილადებში. რაც უფრო მცირეა K ფაქტორი, მით უფრო ახლოს იქნება ნეიტრალური ღერძი ფურცლის შიდა რადიუსთან.

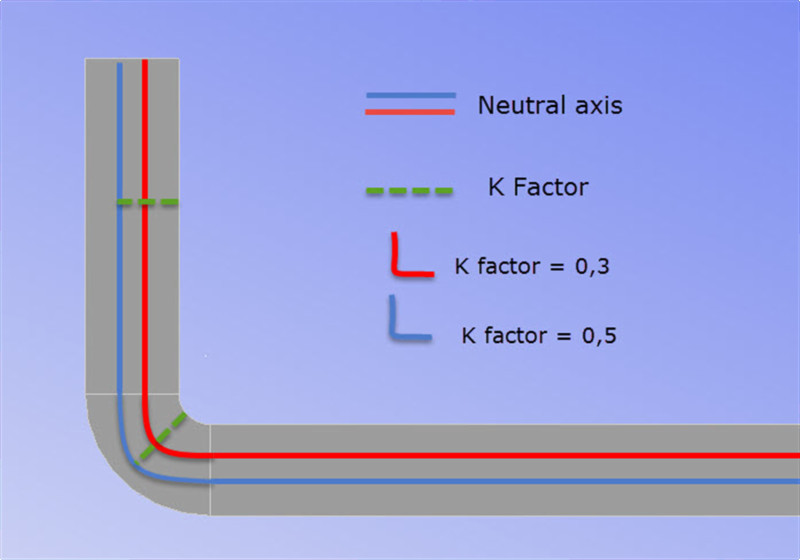
K ფაქტორი = დახვეწილი რეგულირება

K ფაქტორი გავლენას ახდენს ჩვენს გაშლილ ბლანკზე. არა იმდენად, რამდენადაც ნაწილის რადიუსი, მაგრამ შეგვიძლია ვიფიქროთ, როგორც ბლანკების წვრილმანი გამოთვლები.

რაც უფრო მცირეა K ფაქტორი, მით მეტი მასალა ვრცელდება და, შესაბამისად, "გამოდევნილი"... რაც ნიშნავს, რომ ჩვენი ფეხი "დიდი" გახდება.

K ფაქტორის შეფასება

უმეტეს დროს ჩვენ შეგვიძლია გამოვთვალოთ და დავარეგულიროთ K ფაქტორი ჩვენი ცარიელი გამოთვლების სწორად დარეგულირებისას.
ყველაფერი რაც უნდა გავაკეთოთ არის რამდენიმე ტესტი (არჩეულ V გახსნაზე) და გავზომოთ ნაწილის რადიუსი.
იმ შემთხვევაში, თუ თქვენ გჭირდებათ უფრო ზუსტი K ფაქტორის განსაზღვრა, ქვემოთ მოცემულია გაანგარიშება თქვენი მოსახვევისთვის ზუსტი K ფაქტორის დასადგენად.

K ფაქტორი: ფორმულა

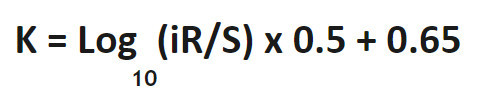
მაგალითის ამოხსნა:

B = 150 + 100 + 60 +BA1 + BA2

K ფაქტორის შეფასება

B1: R/S=2 => K=0,8
B2: R/S=1,5 => K=0,8
ორივე მოსახვევი არის 90° ან ნაკლები:

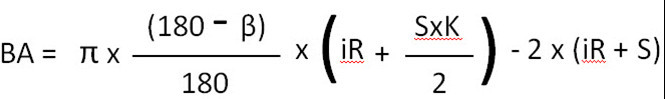
რაც ნიშნავს:

B1 = 3,14 x 0,66 x (6 + ((4×0,8)/2) - 2 x 10
B1 = -4,25
B2 = 3,14 x 0,5 x (8 + ((4×0,8)/2) - 2 x 12
B2 = -8,93

ამიტომ:
B = 150 + 100 + 60 + (-4.25) + (-8.93)
B= 296.8 მმ